Pythonで機械学習を勉強してみた(scikit-learn)②
「Pythonで機械学習を勉強してみた(scikit-learn)」では、機械学習の基本について学びました。
今回は、そのときのコードをベースに、データやモデルの設定を変更しながら、さらに理解を深めていきます。
1. 前回のコード
まずは、前回のコードを振り返ります。
# 必要なライブラリのインポート
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score
# Irisデータセットの読み込み
iris = load_iris()
X = iris.data # 特徴量
y = iris.target # ラベル(クラス)
# 訓練データとテストデータに分割(テストサイズは全体の20%)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 決定木分類器の作成
clf = DecisionTreeClassifier()
# モデルの学習
clf.fit(X_train, y_train)
# テストデータでの予測
y_pred = clf.predict(X_test)
# 予測精度の計算と表示
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)改めて出力を確認すると、以下のようになります。
Accuracy: 1.0
学習モデルの正解率が100%であることが分かります。
ここから、コードの一部を変更し、結果がどのように変化するか試してみます。
2. データ分割方法の変更
ここでは学習方法は変えずに、学習用とテスト用のデータ分割の方法を変えるとどのような影響があるのか見ていきたいと思います。
2.1. 学習データの数
# 訓練データとテストデータに分割(テストサイズは全体の20%)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)現在、150 サンプルのうち 120 サンプルを学習用、30 サンプルをテスト用として使用しています。
test_size を大きくすると、学習データが減少するため、学習の精度が下がると予想できます。
実際に test_size の値を変えて試した結果は以下の通りです。
| test_size | train_samples | test_samples | accuracy |
|---|---|---|---|
| 0.05 | 142 | 8 | 1 |
| 0.1 | 135 | 15 | 1 |
| 0.15 | 127 | 23 | 1 |
| 0.2 | 120 | 30 | 1 |
| 0.25 | 112 | 38 | 1 |
| 0.3 | 105 | 45 | 1 |
| 0.35 | 97 | 53 | 1 |
| 0.4 | 90 | 60 | 0.967 |
| 0.45 | 82 | 68 | 0.971 |
| 0.5 | 75 | 75 | 0.973 |
| 0.55 | 67 | 83 | 0.94 |
| 0.6 | 60 | 90 | 0.978 |
| 0.65 | 52 | 98 | 0.898 |
| 0.7 | 45 | 105 | 0.924 |
| 0.75 | 37 | 113 | 0.929 |
| 0.8 | 30 | 120 | 0.933 |
| 0.85 | 22 | 128 | 0.938 |
| 0.9 | 15 | 135 | 0.956 |
| 0.95 | 7 | 143 | 0.727 |
学習用サンプルが少なくなると正解率が下がる傾向が確認できました。
また、学習データが多いと学習時間も伸びることが予想できるので試してみたいと思います。
Iris データセットではサンプル数が少なく変化が分かりにくいため、ここからはscikit-learn の make_classification() を用いて大規模なデータセットを生成しテストしたいと思います。
以下のコードで、サンプル数100,000、30の特徴量、3つのクラスのデータセットを生成します。
X, y = make_classification(
n_samples=100000, n_features=30, n_informative=20, n_classes=3, random_state=42
)以降はこのデータセットを用いて実験を進めます。(特に指定がなければtest_sizeは0.2)
このデータセットで実施した実験結果は以下の通りです。
| test_size | train_samples | test_samples | accuracy | train_time (s) |
|---|---|---|---|---|
| 0.05 | 95000 | 5000 | 0.801 | 4.605 |
| 0.1 | 90000 | 10000 | 0.792 | 4.1906 |
| 0.15 | 85000 | 15000 | 0.788 | 3.833 |
| 0.2 | 80000 | 20000 | 0.788 | 3.649 |
| 0.25 | 75000 | 25000 | 0.788 | 3.849 |
| 0.3 | 70000 | 30000 | 0.785 | 3.6895 |
| 0.35 | 65000 | 35000 | 0.776 | 2.921 |
| 0.4 | 60000 | 40000 | 0.781 | 2.921 |
| 0.45 | 55000 | 45000 | 0.776 | 2.436 |
| 0.5 | 50000 | 50000 | 0.772 | 2.066 |
| 0.55 | 44999 | 55001 | 0.768 | 2.0056 |
| 0.6 | 40000 | 60000 | 0.768 | 1.62 |
| 0.65 | 35000 | 65000 | 0.76 | 1.362 |
| 0.7 | 30000 | 70000 | 0.759 | 1.1062 |
| 0.75 | 25000 | 75000 | 0.755 | 1.059 |
| 0.8 | 20000 | 80000 | 0.741 | 0.703 |
| 0.85 | 15000 | 85000 | 0.731 | 0.484 |
| 0.9 | 10000 | 90000 | 0.715 | 0.312 |
| 0.95 | 5000 | 95000 | 0.689 | 0.134 |
この表から、学習用データが多いほど学習時間が長くなる一方で、必ずしも正解率が大幅に向上するわけではないことが分かります。
また、Iris データセットでは正解率が100%に達したのに対し、この大規模データセットでは最高でも約80%にとどまり、データの量が全てではないこともわかりました。
2.2 データ分割のランダム性
次に、random_state の影響を確認します。
random_state を固定すると、毎回同じようにデータを分割できます。
では、random_state を固定しない場合はどうなるのでしょうか。
以下は、サンプル数を5000から100000まで変化させ、random_state を固定せずにそれぞれ100回ずつ試行した結果です。
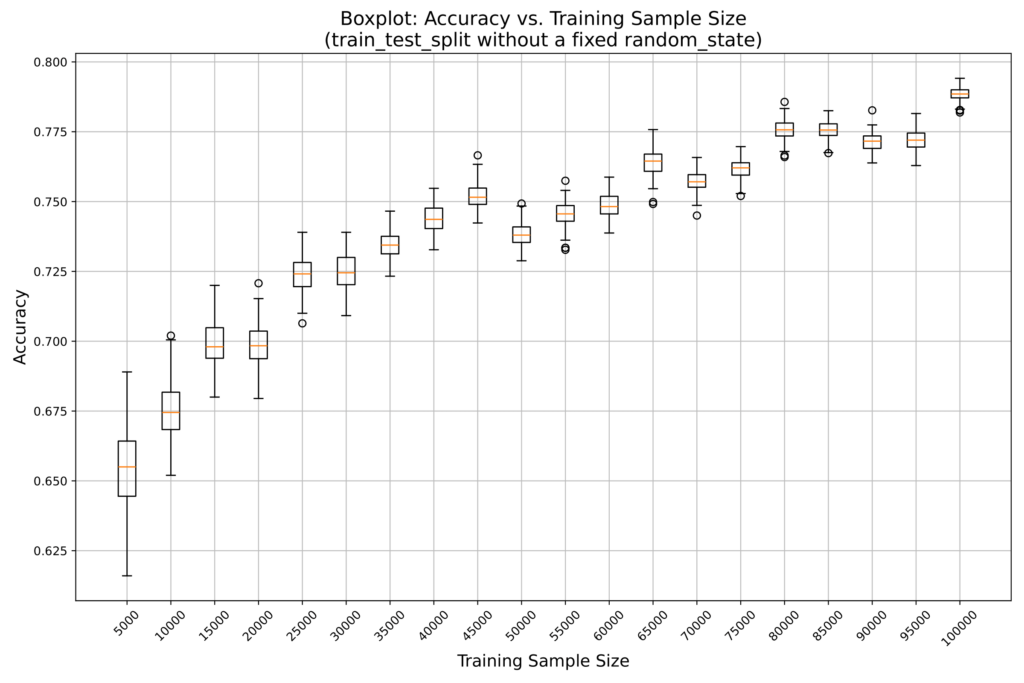
この結果から、random_state を固定しないと、試行ごとに結果にばらつきが生じることが分かりました。
また、サンプル数が増えるほど、ばらつきが少なくなる傾向も確認できます。
したがって、再現性や再利用性を高めるには random_state を固定することが重要であり、一定の結果に収束させるためには十分なデータ量が必要であることが分かります。
3. 学習手法の変更
ここでは学習方法の違いによる影響を見ていきたいと思います。
3.1. 決定木分類のパラメータ
# 決定木分類器の作成
clf = DecisionTreeClassifier()まず、決定木分類の手法でパラメータを変更すると、どの程度違いが出るのかを確認してみます。
すべてのパラメータを試すのは大変なため、下記リファレンスを参考に、一部のオプションを組み合わせて実験を行います。
DecisionTreeClassifier — scikit-learn 1.6.1 documentation
今回は、以下の8つのパラメータを選択しました。
- criterion: 分割品質を評価する指標(例: ‘gini’, ‘entropy’, ‘log_loss’)
- splitter: 各ノードで最適またはランダムな分割を選ぶ戦略
- max_depth: 決定木の最大深さ(Noneの場合は制限なし)
- min_samples_split: 内部ノードを分割するための最小サンプル数
- min_samples_leaf: 葉ノードに必要な最小サンプル数(過学習防止に有用)
- max_features: 分割時に検討する特徴量数(Noneは全特徴量を使用)
- max_leaf_nodes: 葉ノードの最大数で木の複雑さを制限
- ccp_alpha: コスト複雑度剪定パラメータ(大きいほど剪定が強くなる)
これらのパラメータがどのような影響を与えるのか、適切な値が何かはまだ分かりません。
そこで、まずは以下の値を設定し、すべての組み合わせを総当たりで試してみます。
criterions = ['gini', 'entropy', 'log_loss']
splitters = ['best', 'random']
max_depths = [None, 5, 10, 15]
min_samples_splits = [2, 5, 10]
min_samples_leafs = [1, 5, 10]
max_features_list = [None, "sqrt", "log2"]
max_leaf_nodes_list = [None, 10, 20]
ccp_alphas = [0.0, 0.01]上記オプションの組み合わせは3,888通りあってすべて載せると多すぎるので、ここでは特徴的な結果のみを抜粋して記載します。
| criterion | splitter | max_depth | min_samples_split | min_samples_leaf | max_features | max_leaf_nodes | ccp_alpha | Accuracy | Training Time (sec) | |
|---|---|---|---|---|---|---|---|---|---|---|
| Best Accuracy | entropy | best | 15 | 2 | 10 | nan | 0 | 0.808 | 7.06518 | |
| Worst Accuracy | gini | best | nan | 2 | 1 | log2 | 10 | 0.01 | 0.33175 | 0.336704 |
| Longest Training Time | log_loss | best | 15 | 10 | 10 | nan | 0.01 | 0.62895 | 10.3131 | |
| Shortest Training Time | gini | random | nan | 2 | 5 | log2 | 10 | 0 | 0.4907 | 0.0380671 |
| Default Combination | gini | best | nan | 2 | 1 | nan | 0 | 0.78975 | 5.87902 |
この結果から、パラメータを変えるだけで正解率の最小値と最大値には 0.47625 の差があり、学習時間は最長と最短で 10.275秒 の違いがあることが分かります。
また、学習時間を長くすれば正解率が必ず向上するわけではなく、デフォルト設定が必ずしも最も高いスコアを出すとは限りません。
ただし、今回の結果を見る限りでは、デフォルトの設定が正解率と学習時間のバランスが良いように感じました。
したがって、目的や要件に応じてデータの特性や正解率と学習時間のバランスを考慮しながら、適切なパラメータを選択することが重要だと言えます。
3.2. 様々なアルゴリズム
決定木を用いた分類でさまざまなパラメータを試しましたが、ここでは決定木以外のアルゴリズムも試してみます。
今回使用するデータセットは、scikit-learn の make_classification 関数を用いて生成したもので、教師あり学習の分類タスクを想定しています。
そのため、教師あり学習の分類アルゴリズムを使用してモデルを学習させます。
今回試すアルゴリズムは以下の通りです。
- 線形モデル:入力データの各特徴を単純に組み合わせ、直線的な境界で分類します。
- Ridge Classifier:L2正則化を用いて、過学習を抑えながら線形な分類境界を学習します。
- SGD Classifier:確率的勾配降下法により、大規模データでも高速に学習できます。
- Passive Aggressive:誤分類した場合にのみパラメータを更新し、効率的に学習を行います。
- Perceptron:基本的な線形分類アルゴリズムで、データが順次更新される中で学習を進めます。
- Logistic Regression:各クラスの所属確率を計算し、最も高い確率のクラスを予測します。
- 識別分析:各クラスのデータ分布を前提として、分布の違いを利用し分類境界を作ります。
- Quadratic Discriminant Analysis (QDA):クラスごとの分散を個別に考慮し、より柔軟な非線形な境界を構築します。
- Linear Discriminant Analysis (LDA):データ全体の分散とクラスごとの分散の比から線形の境界を見つけます。
- SVM系:データと分類境界との距離(マージン)を最大化し、誤分類を最小化する強力な手法です。
- Support Vector Machine (SVC):カーネル手法により非線形な境界も学習でき、複雑なデータに対応します。
- Linear SVC:線形な境界を高速に求める方法で、特に高次元データで有効です。
- NuSVC:サポートベクターの数や誤分類率のバランスを直接調整できる柔軟な手法です。
- 近傍法:近くのデータ点の情報をもとに、新しいデータのクラスを直感的に決める方法です。
- K-Nearest Neighbors (KNN):指定された近傍のデータ点の多数決でクラスを決定します。
- Nearest Centroid:各クラスの重心(セントロイド)との距離を計算し、最も近いクラスに分類します。
- ナイーブベイズ:各特徴が互いに独立であると仮定し、確率に基づいてクラスを予測します。
- GaussianNB:各特徴が正規分布に従うとみなし、クラスごとの確率を計算します。
- BernoulliNB:特徴が0か1のような二値情報の場合に適した手法です。
- 木ベースモデル:条件に基づいた分割(ルール)でデータをツリー状に分類する方法です。
- Decision Tree:データの各特徴に対して閾値を設定し、順次分割することで分類ルールを作成します。
- アンサンブル:複数のモデルの予測結果を組み合わせ、個々の弱点を補完し高い精度を目指します。
- HistGradient Boosting:データをビン分けして計算負荷を軽減しながら、勾配ブースティングを効率化します。
- Extra Trees:ランダム性を強化した複数の決定木を作り、結果を統合して予測します。
- AdaBoost:誤分類されたデータに重点を置き、後続のモデルで修正を試みます。
- Bagging:データのサブセットを使って複数のモデルを構築し、平均化により安定した予測を実現します.
- Random Forest:多数の決定木を構築し、その結果の多数決または平均で予測を行います.
- Gradient Boosting:前のモデルの誤差を補う形で、順次モデルを追加し強力な予測器を作ります。
- ニューラルネットワーク:多層構造で複雑な非線形関係を学習し、抽象的なパターンを捉えます。
- MLP Classifier:複数の隠れ層を持つネットワークで、入力データの複雑なパターンを学習して分類します。
- メタ推定器:複数の基本モデルの予測を組み合わせ、単独のモデルよりも高い性能を実現します。
- Voting Classifier:各モデルの予測結果を集約し、多数決や平均で最終的な予測を行います。
- Stacking Classifier:各モデルの出力を新たな入力特徴として利用し、別の学習器で最終判断を下します。
- キャリブレーション:モデルの予測する確率の信頼度を調整し、実際のクラス分布に近づけるための手法です。
- Calibrated Classifier:元の分類器の出力確率を補正し、より現実的な予測を実現します。
- ベースライン:高度な手法と比較するための、シンプルな予測モデルです。
- Dummy Classifier:単純なルールに基づいて予測し、他のモデルの性能評価の参考とします。
正直、これだけでは何を言ってるのかさっぱりわかりません。
そのため実際にそれぞれのアルゴリズムで正解率や学習時間にどのような違いが出るのかを確認してみます。
基本的にデフォルトのパラメータを使用していますが、一部のモデルでは警告を回避するために最低限のパラメータを指定しています。
また、基本モデルとしてメタ推定器には Logistic Regression, Decision Tree, Support Vector Machine を、キャリブレーションには Logistic Regression を使用しています。
各モデルの正解率と学習時間は以下の通りです。
| Group | Model | Accuracy | Training Time (sec) |
|---|---|---|---|
| 線形モデル | Ridge Classifier | 0.7037 | 0.3199 |
| 線形モデル | SGD Classifier | 0.6716 | 5.5137 |
| 線形モデル | Passive Aggressive | 0.6434 | 0.8979 |
| 線形モデル | Perceptron | 0.5636 | 1.1462 |
| 線形モデル | Logistic Regression | 0.7018 | 1.3891 |
| 識別分析 | Quadratic Discriminant Analysis | 0.9588 | 0.3409 |
| 識別分析 | Linear Discriminant Analysis | 0.7034 | 0.7772 |
| SVM系 | Support Vector Machine | 0.9762 | 144.432 |
| SVM系 | Linear SVC | 0.7038 | 3.6537 |
| SVM系 | NuSVC | 0.9075 | 674.639 |
| 近傍法 | K-Nearest Neighbors | 0.9684 | 2.8635 |
| 近傍法 | Nearest Centroid | 0.6528 | 1.6627 |
| ナイーブベイズ | GaussianNB | 0.7087 | 0.4032 |
| ナイーブベイズ | BernoulliNB | 0.6293 | 0.3276 |
| 木ベースモデル | Decision Tree | 0.7895 | 6.9506 |
| アンサンブル | HistGradient Boosting | 0.9407 | 7.6067 |
| アンサンブル | Extra Trees | 0.947 | 15.6462 |
| アンサンブル | AdaBoost | 0.6378 | 25.6874 |
| アンサンブル | Bagging | 0.88 | 47.3136 |
| アンサンブル | Random Forest | 0.9372 | 84.8234 |
| アンサンブル | Gradient Boosting | 0.8366 | 415.221 |
| ニューラルネットワーク | MLP Classifier | 0.9813 | 213.853 |
| メタ推定器 | Voting Classifier | 0.8959 | 548.771 |
| メタ推定器 | Stacking Classifier | 0.7742 | 64.9572 |
| キャリブレーション | Calibrated Classifier | 0.7018 | 4.0351 |
| ベースライン | Dummy Classifier | 0.3317 | 0.0466 |
この結果から、アルゴリズムによって正解率や学習時間が大きく異なることが分かります。
同じグループのモデルでも、計算コストや精度に差があり、学習時間が長いからといって必ずしも高精度とは限らないことが確認できました。
例えば、Gradient Boosting は学習に 415秒以上かかって正解率が0.8366の一方で、Quadratic Discriminant Analysis は 0.34秒で0.9588の正解率を達成しており、モデル選択では精度と計算コストのバランスを考慮することが重要だと言えます。
・Dummy Classifier はスコアが低いですが、これは他のモデルの性能を測るための「ベースライン」です。
ランダムな分類よりも高い精度が出ているかを確認する指標として機能します。
今回は教師あり学習の分類アルゴリズムを使用しましたが、データの特性によっては教師なし学習や時系列モデルなど、別の手法を選択する必要があります。
アルゴリズムを選ぶときはデータの特性に応じた選定はもちろん、精度が高いからという理由だけでなく、学習時間やモデルの解釈のしやすさも考慮することが大切だと感じました。
4. 最後に
アルゴリズムによって結果に差が出るのはもちろん、同じアルゴリズムでもパラメータの設定次第で大きく性能が変わることが分かりました。
そのため、データセットに応じて最適なアルゴリズムやパラメータを選ぶのは容易ではありません。
そして単純な精度だけでなく、要件に応じて計算時間やコストのバランスを考慮しながら適切に選択することも重要です。
ぜひ、さまざまなパターンを試しながら、最適な組み合わせを見つけてみてください!
